简体中文
繁體中文
English
Pусский
日本語
ภาษาไทย
Tiếng Việt
Bahasa Indonesia
Español
हिन्दी
Filippiiniläinen
Français
Deutsch
Português
Türkçe
한국어
العربية
Exponential Moving Average (EMA) คืออะไร?
บทคัดย่อ:ดังที่เราได้กล่าวไปแล้วในบทเรียนที่แล้ว ค่าเฉลี่ยเคลื่อนที่ธรรมดาสามารถบิดเบือนได้ด้วยเดือยแหลม เราจะเริ่มต้นด้วยตัวอย่าง
Exponential Moving Average (EMA) คืออะไร?
ดังที่เราได้กล่าวไปแล้วในบทเรียนที่แล้ว ค่าเฉลี่ยเคลื่อนที่ธรรมดาสามารถบิดเบือนได้ด้วยเดือยแหลม เราจะเริ่มต้นด้วยตัวอย่าง
สมมติว่าเราพล็อต SMA 5 งวดในกราฟรายวันของ EUR/USD
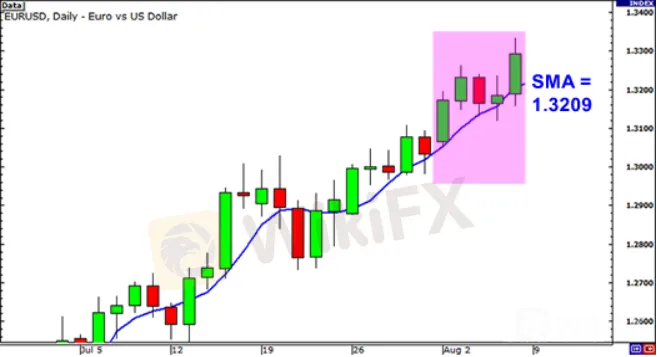
ราคาปิดสำหรับ 5 วันที่ผ่านมามีดังนี้:
วันที่ 1: 1.3172
วันที่ 2: 1.3231
วันที่ 3: 1.3164
วันที่ 4: 1.3186
วันที่ 5: 1.3293
ค่าเฉลี่ยเคลื่อนที่อย่างง่ายจะคำนวณดังนี้:
(1.3172 + 1.3231 + 1.3164 + 1.3186 + 1.3293) / 5 = 1.3209
ง่ายพอใช่มั้ย?
จะเกิดอะไรขึ้นถ้ามีรายงานข่าวในวันที่ 2 ที่ทำให้ค่าเงินยูโรอ่อนค่าลงทั่วกระดาน
ทำให้ EUR/USD ดิ่งลงและปิดที่ 1.3000 เรามาดูกันว่าสิ่งนี้จะมีผลกระทบต่อ SMA 5 งวดอย่างไร
วันที่ 1: 1.3172
วันที่ 2:1.3000
วันที่ 3: 1.3164
วันที่ 4: 1.3186
วันที่ 5: 1.3293
ค่าเฉลี่ยเคลื่อนที่อย่างง่ายจะคำนวณดังนี้:
(1.3172 + 1.3000 + 1.3164 + 1.3186 + 1.3293) / 5 = 1.3163
ผลลัพธ์ของ Simple Moving Average จะต่ำกว่ามาก และจะทำให้คุณเข้าใจว่าราคากำลังลดลงจริง ๆ แต่ว่าในความเป็นจริง วันที่ 2 เป็นเพียงเหตุการณ์ที่เกิดขึ้นครั้งเดียวที่เกิดจากผลลัพธ์ที่ไม่ดีของรายงานทางเศรษฐกิจ
ประเด็นที่เรากำลังพยายามทำก็คือบางครั้งเส้นค่าเฉลี่ยเคลื่อนที่แบบธรรมดาอาจเรียบง่ายเกินไป
ถ้ามีวิธีที่คุณสามารถกรองเดือยแหลมเหล่านี้ออกไปได้ คุณจะได้ไม่เข้าใจผิด
อืม… รอสักครู่… ใช่มีวิธี!
เรียกว่าเส้นค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียล! (Exponential Moving Average)
ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียล (EMA) ให้น้ำหนักในช่วงเวลาล่าสุดมากกว่า
ในตัวอย่างด้านบนของเรา EMA จะให้น้ำหนักมากขึ้นกับราคาของวันล่าสุด ซึ่งก็คือวันที่ 3, 4 และ 5
นี่หมายความว่าการเพิ่มขึ้นอย่างรวดเร็วในวันที่ 2 จะมีมูลค่าน้อยกว่าและจะไม่ส่งผลกระทบอย่างมากต่อเส้นค่าเฉลี่ยเคลื่อนที่เหมือนกับที่เราคำนวณหาค่าเฉลี่ยเคลื่อนที่แบบธรรมดา
หากคุณคิดเกี่ยวกับมัน สิ่งนี้สมเหตุสมผลมากเพราะสิ่งนี้ไม่ได้เน้นย้ำถึงสิ่งที่เทรดเดอร์กำลังทำเมื่อเร็วๆ นี้มากกว่า
ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียล (EMA) กับ ค่าเฉลี่ยเคลื่อนที่แบบธรรมดา (SMA) (Exponential Moving Average (EMA) vs. Simple Moving Average (SMA))
มาดูกราฟ 4 ชั่วโมงของ USD/JPY เพื่อเน้นว่าเส้นค่าเฉลี่ยเคลื่อนที่อย่างง่าย (SMA) และค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียล (EMA) จะดูเคียงข้างกันบนกราฟอย่างไร

สังเกตว่าเส้นสีแดง (30 EMA) ดูเหมือนจะเป็นราคาที่ใกล้กว่าเส้นสีน้ำเงิน (30 SMA) อย่างไร
ซึ่งหมายความว่าแสดงการเคลื่อนไหวของราคาล่าสุดได้แม่นยำยิ่งขึ้น คุณอาจเดาได้ว่าทำไมสิ่งนี้ถึงเกิดขึ้น
เป็นเพราะค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียลให้ความสำคัญกับสิ่งที่เกิดขึ้นเมื่อเร็วๆ นี้มากกว่า
เมื่อทำการเทรด การดูว่าเทรดเดอร์กำลังทำอะไรอยู่ตอนนี้ มากกว่าสิ่งที่พวกเขาทำเมื่อสัปดาห์ที่แล้วหรือเดือนที่แล้ว
ข้อจำกัดความรับผิดชอบ:
มุมมองในบทความนี้แสดงถึงมุมมองส่วนตัวของผู้เขียนเท่านั้นและไม่ถือเป็นคำแนะนำในการลงทุน สำหรับแพลตฟอร์มนี้ไม่รับประกันความถูกต้องครบถ้วนและทันเวลาของข้อมูลบทความ และไม่รับผิดชอบต่อการสูญเสียใด ๆ ที่เกิดจากการใช้ข้อมูลในบทความ
WikiFX โบรกเกอร์
VT Markets
Pepperstone
EC Markets
GO MARKETS
Tickmill
FXTM
VT Markets
Pepperstone
EC Markets
GO MARKETS
Tickmill
FXTM
WikiFX โบรกเกอร์
VT Markets
Pepperstone
EC Markets
GO MARKETS
Tickmill
FXTM
VT Markets
Pepperstone
EC Markets
GO MARKETS
Tickmill
FXTM
ข่าวล่าสุด
ค่าเฉลี่ยเคลื่อนที่ (Moving Averages)
สรุป: แนวรับและแนวต้านการซื้อขาย
กราฟแท่งเทียนพร้อมแนวรับและแนวต้าน (Candlesticks with Support and Resistance)
วิธีใช้ส่วนขยาย Fibonacci เพื่อรู้ว่าเมื่อใดควรทำกำไร
Fibonacci Retracement นั้นไม่สามารถป้องกันได้
วิธีการใช้ Fibonacci Retracement กับ Trend Lines
วิธีการใช้ Fibonacci Retracements
กายวิภาคของแท่งเทียนญี่ปุ่น
สรุป: การใช้เส้นค่าเฉลี่ยเคลื่อนที่ (Using Moving Averages)
วิธีการเทรดขาลงและขาขึ้น
คำนวณอัตราแลกเปลี่ยน


